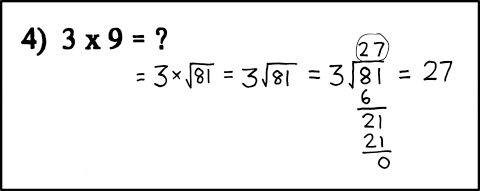
via a kind reader. Related: Connected Math, Math Forum audio/video, the successful Seattle Discovery Math lawsuit and the Madison School District Math Task Force (SIS links).

e = get, head
Dive into said
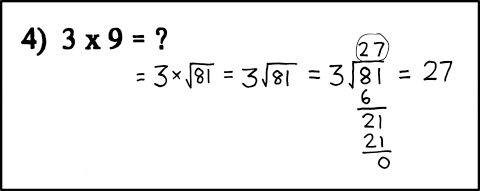
via a kind reader. Related: Connected Math, Math Forum audio/video, the successful Seattle Discovery Math lawsuit and the Madison School District Math Task Force (SIS links).

e = get, head
Dive into said
This is over my head. Could somebody explain this posting to me and how it is relevant to Connected Math, Discovery Math or any other math curriculum?
OK, I’ll bite. What is the value of turning 9 into the square root of 81? I mean, from a computational perspective, what’s the point? What was the lesson supposed to teach? I’m so confused…
Hi Lucy,
The example is gibberish, of course. To explain this “problem” algebraically, the equation to solve is
What are the values of X such that
3X = X^2/3, where X^2 mean the square of X.
implies
9X = X^2
implies
X^2 – 9X = 0
implies
X(X-9) = 0
This equation is true if X = 0, or X = 9.
Somebody must have thought the original post contributed something important to the discussion. It doesn’t!
Jim: Since you posted this, can you do two things for those of us reading here: (a) state your point about making the post? and (b) Can you tell us the *context* in which this was originally presented?
A kind reader’s email (with attachment) prompted the post, which, frankly, made me wonder what, if anything is happening to MMSD math programs including middle schools, given the controversial implementation of Connected Math.
Mitchell, you served on the Madison School District’s Math Task Force:
http://boeweb.madison.k12.wi.us/math/
Perhaps you might update readers on the practical outcome of the Task Force Report? Has anything changed in the adult to student Math approach in the MMSD? What has been implemented?
I can tell you one disturbing thing about middle school math from my seventh-grader’s experience last year.
He FINALLY brought home a math workbook (they have a different text/workbook combo for each “subject” they’re learning – angles, ratios, whatever). I checked his work after he did the homework (which he rarely, RARELY had). Then I poked through the chapter to see how they were teaching this subject. He only had to do two pages – I don’t remember if it was 10 problems or what, but something teeny like that.
That was followed by two or three more pages of additional problems that were labeled differently – something like “challenge problems” or something. I’m afraid I don’t remember the specifics. I ended up arguing with my son, who says they’re not SUPPOSED to do those, when I suggested he give them a try.
I emailed his teacher and asked about those problems. She says that MMSD (or Feds?) have crammed so much into what the kids have to learn in seventh grade that the teachers simply can’t make it through all of each book/workbook, because there are so darn many of them. They just do the first few problems and move on. That’s all they have time to do.
When I asked about why kids couldn’t be asked/encouraged to do the problems for HOMEwork, it wasn’t really answered. I guess that would mean someone would have to find the time to provide the answers the next day.
I wanted to press it, but my kids’ teachers already think I’m a pain in the ass (too interfering). And besides, I can never get him to bring HOME any work anyway. This was a rare moment.
The relevance of the initial post makes perfect sense to me. In order to develop higher level thinking skills and for children to construct deeper understanding, the constructivist textbooks mentioned lead the student to learn this way.
The folly is that 3 x 9 should have been memorized in 2nd or 3rd grade and the mmsd student should be well on their way to algebra and beyond.
All in all, the original post was a nice snapshot of all that is wrong with most math instruction being used now.
The key issue, unless I really missed something, is that the “problem” makes no sense whatsoever. It’s all wrong in the most fundamental ways.
3 x 9 = 3 x sqrt(81)
Then the next step is to remove the “x’ symbol because concatenation can represent multiplication.
However, the next step changes the definition of the representation from meaning multiplication to meaning division. This is mathematical nonsense, though the equality happens to be correct.
The equality in this example is true only for the values of 0 and 9, not for any N.
Show me any math book, constructivist or not, which purports to allow or encourage this nonsense.
If the purpose of this problem is to make students aware of and be able to detect changes in meaning of representations of concepts, then perhaps the example could be useful. If that is the case, then I’ve got another problem just like it.
101 modulo 2 = 101 modulo 2.
Where the 101 of the left-hand side is the representation of the decimal number 5 in binary (that is, base 2), for which the remainder (modulo) when divided by 2 is 1.
And 101 modulo 2 on the right-hand side is the decimal number one hundred one (101 base 10) modulo 2 and says that the result is also 1.
The resulting equality is true, but mathematically silly.
Larry,
Here are several “purported” examples you asked for. I’ll load up Mr. Zellmer’s server with more if you like. Also search russian peasants algortihm for interesting perspective.
http://www.youtube.com/watch?v=eKld7lQHKRg&feature=player_embedded
http://www.lewrockwell.com/taylor/taylor78.html
As a side mental exercise, I have no problem with briefly exposing students to roundabout ways to find answers. We run into problems, though, when it is the primary algorithm used to solve a problem. Besides, we simply do not have the time to waste.
oops, forgot this one
http://www.youtube.com/watch?v=Tr1qee-bTZI
rcs,
You stated that original problem commented on makes sense to you, and I asked for any examples from any books anywhere that would purport to accept the example as anything but nonsense. You didn’t do that, instead changed the subject and listed opinions of others who share your displeasure with current math teaching methods.
If you think the example that this entry makes sense, please explain yourself, and wherein it does make sense to you.
What I find problematic about these math wars is that, for the most part, those most emotional about them are those least qualified to comment. Math understanding in the US is quite awful, and most who comment seem to have only knowledge and know only the algorithms they may have learned badly in elementary school.
I find quite humorous the “weather lady” pushing her agenda of what is the “right” algorithm to use for multiplication and division. However, there are multiple algorithms to getting right answers. When I was a kid, my mother bought me a book on doing mental arithmetic. The author claimed he came up with these algorithms to keep his mind active while in a German concentration camp. I found they worked just as well as the “long” ways I was taught — and I didn’t need pencil and paper to do them.
In this clip of an BBC interview with Richard Feynman, he says the algorithms one learns in school are to allow kids to get the right answers when they don’t understand what they’re doing.
http://www.youtube.com/watch?v=Wwtbh6wcq78&feature=related
Feynman had one of those, once in a century minds, who understood more than most of us could possible dream of, so his comments need to taken with this in mind.
So the issues seem to be teaching to blindly follow one of many algorithms which always works vs teaching for understanding.
We live in a country of scant knowledge and therefore emotional desires to take positions at extremes which cannot be supported by reality.
So it’s either learn multiplication and long division the way we did 60 years ago and not understand why it works, or learn for understanding, even though the result is not being able to get the answer with any facility.
It’s really not either/or, it needs to be both.
When I said it made sense, I meant that it made sense because it was in the context of multiplication from a new-math methodology, which would make sense if you subscribe to that kind of nonsense. Did that make sense?
I did not change the subject. Every day math, connected math, etc do it this way. I do not have them in my library and the publishers don’t show inside of every page on the internet. You know that. Besides, Larry, show me a book that states…”a pancake has 2 sides” Some things are just known, or should be.
The weather lady made my point.
You do not need to know the physics behind how a hammer works to drive a nail. Same with the basics of math. They must be learned quickly so they can be used to advance. I agree with your last sentence, but not the “needs” to be both. It would be nice to have both, but we simply do not have the time. If state schools had the kids from age 3, for 10-12 hours a day, 280 days a year, we might be able to accomplish it.
That we don’t have time is quite silly. There is plenty of time. Time has never been the problem. Approaches that do not work will not work regardless of the time spent.
The arithmetic stuff is not difficult but depends on prior knowledge of the kids, and their maturity, and how well the material is presented.
Good curriculum requires repeated switching back and forth between concrete and symbolic examples and exercises depending on a student’s needs.
I don’t necessarily agree with your analogy re the hammer and nail. Math is not concrete and the basics of math are not trivial, since math is only little-t “true” and not big-t “True”. It is one thing to learn the mechanics of arithmetic like multiplication and division, and quite another to know when multiplication or division makes sense in a given context.
If my memory serves me, the TIMSS studies (of 15 year olds) illustrate that US students fair poorly in problems requiring multi-step solutions. That is, they don’t understand when to apply math and arithmetic algorithms and in what order. Being proficient in long division, or facile on a calculator is simply mostly irrelevant.
The “weather” lady’s preference for long multiplication is really quite frustrating. Her example of 26 x 31 shows the problem.
Especially in multi-step problems, one needs to understand what the approximate answer is before going into the often tedious mechanics of getting the exact answer, even if getting the exact answer is important.
26 x 31 = 806 — this is exactly true. In many real life situations and to determine if something makes sense, I don’t need or want to know the exact answer — the exact answer is not important.
The answer is about 600 (20 x 30). I can get closer by observing that I have about 6 30s, which gives me another 180, or now about 780.
If all a kid learns is the long multiplication method, an algorithm that always works without the need to understand why it works, then they’ve not really learned much. Especially, that the problem can be seen as
(20 + 6) x (30 + 1) and we talk our way to either a good estimate or the exact answer, depending on where you stop with the narrative.
“I’ve got 20 30s for 600, then another 6 30s for 780, and 1 26 left over for 806.” Couldn’t be simpler, don’t need a calculator or pencil and paper. We just need to know the rewrite rules for the math symbols we use.