Moscow Mathematics Festival 2009 - Grade 6. Time: 2 hours
Problem 1. 2009 has the following property: if you switch digits (numbers cannotstart with zero) then the resulting number is always larger. Which is the next largernumber for which this is the case? (3 points)
Problem 2. Divide the two figures below into 8 equal parts. Draw your solution insidethe lower right-hand figure. (4 points)

Problem 3. In a park grew limetrees and maple trees. The maples initially made up60% of the trees. The next spring limetrees were planted were planted in such aquantity that after the planting the maples made up 20% of the trees. But then the next fall maples were planted in such a quantity that maples once again made up 60%of the trees. By how many times did the number of trees grow that year? (6 points) Problem 4. If an octopus has an even number of legs it always tells the truth; if it hasan odd number of legs it always lies.
The green octopus once said to the blue octopus: “I have 8 legs. But you only have 6legs”. “No”, said the blue octopus , “I have 8 legs, and you only have 7 legs”. The violet octopus then said: “The blue octopus actually does have 8 legs. But I have 9 legs!” The striped octopus then entered the conversation and said: “None of you has8 legs – only I have 8 legs”.
Which of the octopi actually has/have 8 legs? (7 points)
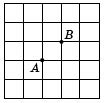
Problem 5. The curious tourist wanted to walk along the streets of the Old City fromthe train station (point A) to her hotel (point B). The tourist wanted her walk to be as long as possible, but did not want to ever reach the same crossing twice. Draw the longest possible path and prove that it is indeed the longest. (7 points)
Problem 6. A) A stingy knight kept golden coins in six chests. Once, when hecounted the coins, he noticed that if one opened any two chests then it was possibleto distribute the coins evenly between the two chests. He also noticed that if one opened any three, four or five chests then it was also possible to divide the coins inthose evenly among the open chests. Suddenly there was a knock on the door, andthe old miser did not know whether it was possible to distribute all the coins evenlyamong all six chests. Is it possible to answer this question without looking in thechests? (5 points)
B) If there were eight chests, and the coins could be evenly distributed in any two,three, four, five, six or seven chests, would the stingy knight then be able to knowwhether he would be able to distribute the coins evenly across all eight chests? (5points)